Kobling mellom testene og håndboka

11.1 Betydningen av multiplikasjon med tall mindre enn 1 (brøk og desimaltall) (8, 9, 10)
11.2 Betydningen av divisjon med tall mindre enn 1 (brøk og desimaltall) (9, 10)

Introduksjon

Når vi multipliserer med et tall mindre enn 1, blir produktet mindre enn den største faktoren. Når vi dividerer med et tall mindre enn 1, blir kvotienten større enn dividenden.

Eksempler på misforståelser og misoppfatninger

Mange elever tror at multiplikasjon gjør svaret større, mens divisjon gjør svaret mindre. Årsaken til det kan være at elevene overfører reglene som gjelder for hele tall, og lar dem gjelde for brøk og desimaltall.

• «Hva er størst, 100 – `(1)/(2)` eller 100 ∙ `(1)/(2)`? «Det må være 100 ∙ `(1)/(2)` fordi det er multiplikasjon.»
• «20 : `(1)/(2)` = 40 kan ikke stemme fordi det er divisjon, og da må svaret bli mindre enn 20.»
• «30 : 0,5 kan ikke bli 60 fordi det er mer enn 30.»

Anbefalinger og gode spørsmål

Beregninger basert på situasjoner i hverdagen er ofte tydelige, mens de kan bli mer fjerne og utydelige når de uttrykkes matematisk. Det er for eksempel tydelig at vi kan dele tre hele pizzaer i 12 like store deler, der hver del er en firedel. Sammenhengen mellom det visuelle bildet og regnestykket 3 : `(1)/(4)` = 12 må tydeliggjøres. Oversettelser fra praktiske situasjoner til ord, og videre til symboler, må elevene øve jevnlig på.

Diskuter med elevene:

Argumenter fra tolkninger av hverdagssituasjoner

• Multiplikasjon: Halvparten av 30 er 15.
  `(1)/(2)` ∙ 30 = 30 ∙ `(1)/(2)` = 15
• Divisjon: Hvor mange halve epler blir det hvis vi deler 10 epler i halvdeler?
  10 : `(1)/(2)` = 20

Argumenter fra operasjoner med hele tall

• • Multiplikasjon: 12 ∙ 3 = ? Spør: «Hva er 12 ganger 3?» 
  Deretter 12 ∙ `(1)/(4)` = ? Spør: «Hva er 12 ganger en firedel?»
• • Divisjon: 8 : 4 = ? Spør: «Hvor mange firere er det i 8?»
• • 8 : `(1)/(3)` = ? Spør: «Hvor mange tredeler er det i 8?»

Argumenter fra motsetninger

• Kan 6 ∙ 3 og 6 : 3 gi samme svar? Nei.
• Kan 6 ∙ `(1)/(3)` og 6 : `(1)/(3)` gi det samme svar? Nei.

Argumenter fra mønster

Fullfør disse multiplikasjons- og divisjonstabellene:

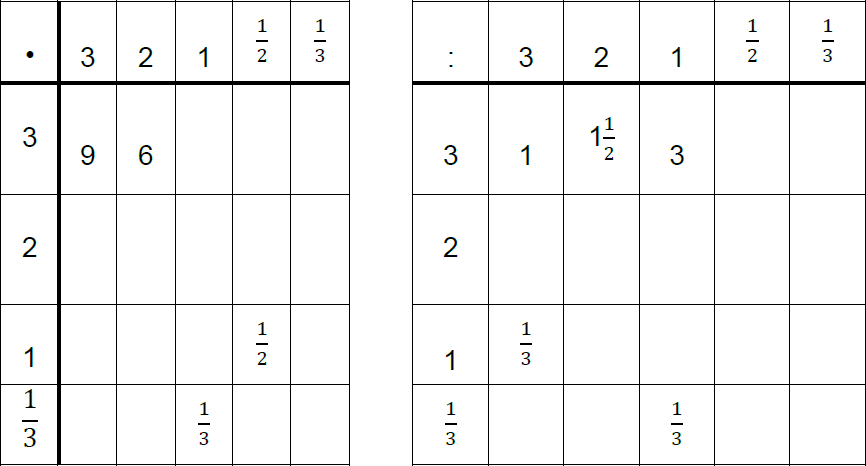
Mønsteret antyder at tallverdiene alltid avtar eller vokser langs en rad. Ta utgangspunkt i betydningen av brøker og desimaltall.

Multiplikasjon:
12 ∙ `(3)/(4)` betyr (12 ∙ 3) : 4. Det er 36 : 4, som er 9. Derfor er 12 ∙ `(3)/(4)` = 9.

Divisjon:
7 : 0,1 = 7 : `(1)/(10)` = 7 ∙ `(10/1)` = 7 ∙ 10 = 70

• Bruk noen av argumentene fra avsnittet over. Gi eksempler og be elevene lage flere.
• Gi elevene situasjoner fra hverdagslivet (og regnefortellinger) som de må oversette til matematiske uttrykk. Eksempel: «Hver person vil spise to tredeler av en pizza. Hvor mange pizzaer trenger vi til 6 personer?»
• Gi regnestykker til elevene som de skal sette inn i hverdagssituasjoner (eller regnefortellinger). For eksempel:
  • 8 ∙ `(1)/(2)` = 4
  • 25 ∙ 0,5 = 12,5
  • 60 ∙ `(3)/(4)` = 45
  • 8 : `(1)/(2)` = 16
  • 25 : 0,5 = 50
  • 60 : `(3)/(4)` = 80