Kapittel 5.6 - Brøk

Kobling mellom håndboka og kartleggingstestene

5.6 Forstå likeverdige brøker (8, 9, 10)

Introduksjon

Å forstå hva som menes med likeverdige brøker, er en sentral del av tallforståelse. To brøker er likeverdige hvis de har lik verdi. Den tradisjonelle måten å lage brøker av lik verdi på er å «gange telleren og nevneren med samme tall». Men å lære denne regelen gir ikke nødvendigvis innsikt i hva likeverdige brøker er.

Regler knyttet til symbolbehandling vil bli mer meningsfulle hvis det dreier seg om generalisering av sammenhenger der elevene samtidig bruker konkretiseringsmateriell.

Figur 5.1 viser like store diagram der like stor del av sirkelen er skravert, men brøkene er skrevet på to ulike måter. De skraverte områdene er like, og brøkene er likeverdige.

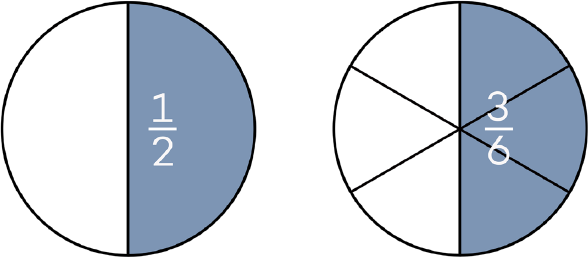
Figur 5.1. Brøksirkler
Figur 5.1. Brøksirkler

Ved å multiplisere den opprinnelige brøken med 1 (f.eks. med `(2)/(2)` eller `(3)/(3)`) får vi likeverdige brøker. For å forstå denne generaliseringen må eleven både vite at 1 = `(2)/(2)` = `(3)/(3)` = `(4)/(4)` ... og kunne multiplisere to brøker, og forstå at `(1)/(2)` ∙ `(3)/(3)` = (1 ∙ 3) : (2 ∙ 3) Å tegne og / eller klippe opp varianter av ulike figurer er da lurt. Det er også viktig å samtale om hva en gjør, og hvilke tallsymboler som inngår i representasjonene.

Eksempler på misforståelser og misoppfatninger

  • Det er ingen brøker med verdi mellom en femdel og to femdeler.
  • Det er ingen brøker mellom en firedel og en tredel.
  • To femdeler er en mer riktig form på en brøk enn seks femtendeler.

Anbefalinger og gode spørsmål

Bruk tid på å få elevene til å forstå hva som menes med likeverdige brøker, og hvorfor de er nyttige. Tegn sirkler og rektangler som elevene deler i 2, 3, 4 og 5. Fortsett å dele disse ytterligere i flere deler (se figur 5.1). Kontroller at elevene forstår at å multiplisere telleren og nevneren med samme tall, er det samme som å multiplisere den opprinnelige brøken med en.

  • Del en sirkel i fire like deler. Skraver en firedel. Del en annen sirkel i firedeler, og del hver av disse firedelene i tre deler. Hvor stor blir hver brøkdel? Skraver en firedel av sirkelen. Hvor mange tolvdeler er det? Fullfør: `(1)/(4)` = `(?)/(12)`, `(1)/(2)` = `(?)/(12)`, `(3)/(4)` = `(?)/(12)`
  • Gjenta øvelsen med andre sirkler og rektangler.
  • Tegn et diagram som viser at `(3)/(5)` = `(6)/(10)`
  • Forklar hva som skjer når vi multipliserer en brøk med `(4)/(4)`.

Forklar hvorfor `(9)/(15)` og `(12)/(20)` har lik verdi.