Kobling mellom testene og håndboka

21.4 Regning med brøk (7, 8, 9, 10)

Introduksjon

Reglene for multiplikasjon og divisjon med brøk virker forholdsvis enkle. Ved multiplikasjon skal tellerne multipliseres sammen og nevnerne multipliseres sammen. Ved divisjon snur en den siste brøken opp ned, og går deretter videre som for multiplikasjon. Men denne mekaniske framgangsmåten gir ikke elevene innsikt i om svaret de kommer fram til, er rimelig. Alle regler som ikke gir mening for elevene, har svakheter.

Forklaringer på multiplikasjon av brøk henger mye sammen med forståelse av språk og symboler. Betydningen av «3 av 4» og «3  4» er sentral, og ikke så opplagt for elevene som en skulle tro. Dette må elevene ha innarbeidet for hele tall, før de kan finne mening i regneoperasjoner med brøk. Reglene for multiplikasjon av brøk kan da utvikles på følgende måte. Vi viser bare noen få eksempler. Det er nødvendig med mange eksempler for å etablere det generelle mønsteret.

• Hele tall multiplisert med brøk: 2 ∙ `(1)/(3)` = `(2)/(3)`
• Brøk multiplisert med hele tall: `(1)/(4)` av 2
• En enhetsbrøk multiplisert med en enhetsbrøk: `(1)/(2)` av `(1)/(2)`
• En enhetsbrøk multiplisert med en generell brøk: `(1)/(2)` av `(2)/(3)`
• En generell brøk multiplisert med en generell brøk:

En illustrasjon kan hjelpe elever til å se multiplikasjon av to hele tall som arealet av et rektangel. Illustrasjonen under viser 3 ∙ 4.

Antall rader blir multiplisert med antall søyler. Her er et tilsvarende bilde for `(2)/(3)` ∙ `(4)/(5)`:

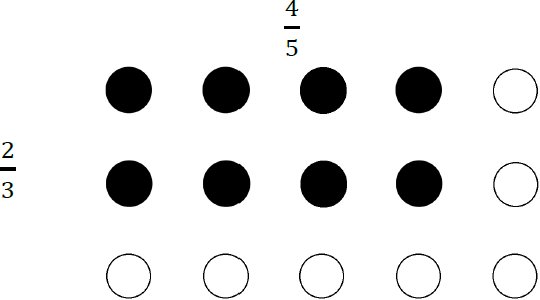
To tredeler av 4 av 5 søyler er svarte. Da er 8 av 15 sirkler svarte. Resultatet viser tydelig at (2 ∙ 4) av (3 ∙ 5) sirkler er svarte. Noen synes dette er til hjelp. Framgangsmåten for divisjon med brøk kan forklares eller begrunnes på samme måte. Denne forklaringen er avhengig av at elevene vet at

• `(a)/(1)` = a
• `(a)/(b)` ∙ `(b)/(a)` = 1

Når vi multipliserer telleren og nevneren med samme tall, blir ikke verdien av brøken endret.

Vi ser på eksempelet:

`(3)/(5)` : `(4)/(7)` = `(3)/(5)` ∙ `(7)/(4)` : `(4)/(7)` ∙ `(7)/(4)` (multipliserer telleren og nevneren med `(7)/(4)`) = `(3)/(5)` ∙ `(7)/(4)` : 1 = `(3)/(5)` ∙ `(7)/(4)`

Eksempler på misforståelser og misoppfatninger

Tre vanlige misoppfatninger som gjelder multiplikasjon og divisjon av brøk:

• Reglene for multiplikasjon kan lett forveksles med reglene for addisjon, slik at elevene adderer tellere og nevnere når de skal addere brøker. Eksempel: `(2)/(3)` ∙ `(5)/(7)` = `((2 * 5))/((3 * 7))` slik at `(2)/(3)` + `(5)/(7)` = `((2 + 5))/((3 + 7))`
• Divisjonsregelen er ikke logisk for elevene og stemmer ikke med deres intuisjon. Derfor er det ofte vanskelig å huske hvilken brøk som skal snus opp ned. For eksempel snur de ofte den første brøken når de skal dividere brøker med hverandre.
• Den tredje misoppfatningen er at multiplikasjon «gjør større» og divisjon «gjør mindre». Det er omtalt i kapittel 11 (multiplikasjon og divisjon med tall mindre enn 1).

Anbefalinger og gode spørsmål

• Undervis for å fremme forståelse. I de fleste tilfeller er det å bygge opp bedre forståelse av brøk viktigere enn å lære å dividere brøker.
• Bruk illustrasjoner og konkretiseringsmateriell for brøk (sirkler, rektangler o.l.)