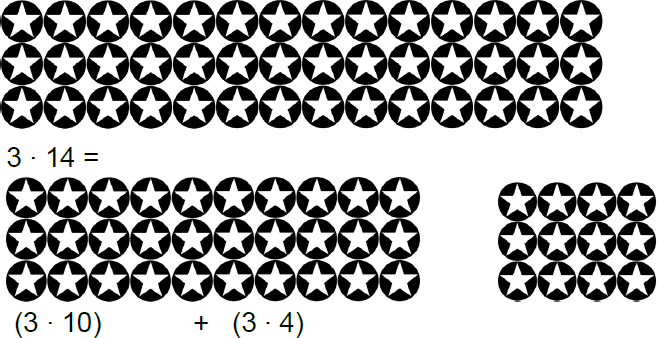Kobling mellom testene og håndboka

21.1 Enkel skriftlig multiplikasjon (6, 7)

Introduksjon

Dette kapitlet handler om multiplikasjon av to- og tresifrede hele tall med et ensifret tall. Mange elever kan gjøre en del slike beregninger i hodet, og alle bør være i stand til å gjøre beregninger med lommeregner. Likevel bør de utvikle en forståelse av prosessen ved også å kunne gjøre slike beregninger med papir og blyant.

På dette stadiet bør elevene ha god forståelse av posisjonssystemet for hele tall opp til 1000 (kapittel 3). De bør også ha god begrepsforståelse av hva multiplikasjon er (underkapittel 10.1–10.4), og spesielt bør de kunne bruke den distributive lov for multiplikasjon (underkapittel 10.8).

Eksempler på misforståelser og misoppfatninger

Mange elever kan miste oversikten over hva de egentlig gjør når de følger en multiplikasjonsalgoritme. Misforståelser og misoppfatninger kan oppstå når oppmerksomheten rettes for mye mot symbolene og oppstillingen, og ikke mot betydningen av beregningene. Da blir det også vanskeligere å vurdere svaret etterpå.

Nesten alle misforståelser innen skriftlig multiplikasjon kommer av:

• Usikkerhet i den lille multiplikasjonstabellen, som fører til feil i enkeltsiffermultiplikasjon
• Mangel på forståelse av posisjonssystemet, som fører til at tallet blir stilt opp feil, eller at minnetallet blir borte eller blir skrevet som et separat siffer
• Mangel på forståelse av den distributive lov for multiplikasjon som fører til addisjon i stedet for multiplikasjon av sifferet på tierplassen. For eksempel at 38∙7= 3 + 8∙7.
• Tar ikke hensyn til sifrenes posisjon, men skriver alle tallene i multiplikasjonen. For eksempel 38 ∙ 7= 2156

Anbefalinger og gode spørsmål

Hvis det er oppstillingen som fører til problemer, må vi snakke med eleven om det, og forklare hvorfor vi skriver utregningene som vi gjør. Oppmuntre eleven til å tenke på hva slags situasjon regnestykket beskriver, og hva svaret skal fortelle. Be elevene gjøre overslag og tenke over om svaret de har fått ved å bruke den skriftlige algoritmen, kan være riktig.

• Kontroller elevens forståelse av posisjonssystemet og multiplikasjon, om han kan den lille multiplikasjonstabellen og skrivemåten for algoritmen for slik multiplikasjon.
• Skill ut den spesielle årsaken til misforståelsen eller misoppfatningen, og arbeid med den.
• Be eleven regne oppgaven både i hodet og på papir, og sammenligne svarene.

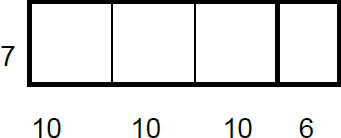
• Bruk oppstillinger i rektangelform for å forklare og begrunne den distributive lov, for eksempel: