Kobling mellom testene og håndboka
15.1 Gjenkjenne multiplikasjon (5)
15.2 Ha automatisert eller raskt kunne rekonstruere det meste av den lille multiplikasjonstabellen (5, 6)
15.3 Ha automatisert eller raskt kunne rekonstruere den lille multiplikasjonstabellen (6, 7, 8, 9, 10)
Introduksjon
I dette kapitlet vil vi ta for oss tabellkunnskaper i multiplikasjon og divisjon. Det vil si den lille multiplikasjonstabellen, og tilsvarende tabellkunnskaper for divisjon.
Det er viktig at elever har automatisert eller raskt kan rekonstruere tabellkunnskapene. Disse ferdighetene er sammen med posisjonssystemet og forståelse av regneoperasjonene selve fundamentet for tallbehandling. Tabellferdighetene er et viktig sluttmål, men må ikke bli overfokusert for tidlig slik at det går på bekostning av forståelsen.
Legg vekt på hoderegningsstrategiene som elevene bruker. Diskuter ulike strategier og det å velge hensiktsmessige strategier. Skap bevissthet om sammenhengene mellom tabellsvarene.
Telling med sprang (5, 10, 15, 20 …) kan være en naturlig fase i oppstarten av arbeid med multiplikasjon. Men i det videre arbeidet bør elevene kunne bruke ulike strategier for ulike gangerekker. Noen eksempler ser du i tabell 15.1.
| Multipla av ... | Strategi | Eksempel |
|---|---|---|
| 2 | Doble | 2 ∙ 7. Det dobbelte av 7 er 14 |
| 3 | Doble og legge til en mengde ekstra | 3 ∙ 7 = 14 + 7 |
| 4 | Doble to ganger | 4 ∙ 7 = 2 ∙ 14 |
| 5 | Halvparten av tigangen | 10 ∙ 7. Halvparten av 70 |
| 6 | Femgangen pluss en mengde ekstra | 6 ∙ 7 = 35 + 7 |
| 7 | Femgangen pluss to mengder ekstra | 7 ∙ 7 = 35 + 14 |
| 8 | Doble tre ganger | 8 ∙ 7. To ganger 7 er 14. To ganger 14 er 28. To ganger 28 er 56. |
| 9 | En mengde mindre enn tigangen | 9 ∙ 7 = 70 – 7 |
Eksempler på misforståelser og misoppfatninger
Det viser seg at elever har to hovedutfordringer knyttet til basisferdighetene:
- De husker dem ikke, og klarer ikke å rekonstruere dem.
- De bruker ikke tabellkunnskapene på en hensiktsmessig måte.
Vær oppmerksom på elever som gjentatte ganger teller videre med 1 for å løse multiplikasjonsstykker. 6 ∙ 4 er «1, 2, 3, 4; 5, 6, 7, 8; 9, 10 …» Disse elevene trenger et gjennomtenkt opplegg for å få mer effektive strategier. Det kan være gjennom aktiviteter og spill, og det må skje før de introduseres for multiplikasjon med større tall.
Mange feil i multiplikasjon henger sammen med sammenblanding av tall (f.eks. 54 og 56), og ineffektive telleteknikker. Når elevene skal regne ut for eksempel 7 ∙ 4, kan de telle med sprang 4, 8, 12 … og telle 6 eller 8 sprang i stedet for 7. Det er viktig å be elever som gjør slike feil, om å forklare eller demonstrere hvordan de teller. Det kan hende de bruker en unøyaktig framgangsmåte uten at de er klar over det. For eksempel kan noen elever begynne å telle fra 0 når de teller med sprang.
Anbefalinger og gode spørsmål
Vi foreslår at gangerekkene introduseres i rekkefølgen 2-gangen, 3-gangen, 1-gangen og 10-gangen, 5-gangen, 4-gangen, 6-gangen, 9-gangen, 8-gangen og 7-gangen, og at punktene nedenfor blir brukt i hver gangerekke.
- Kontroller elevenes forståelse ved å lage rektangulære områder (se kapittel 10) for å representere en av gangerekkene.
- Lag kontekster (praktiske situasjoner). Oppfordre elevene til å lage regnefortellinger der en gangerekke inngår.
- Introduser strategiene for gangerekkene (se tabellen over) gjennom aktiviteter med konkreter og påfølgende diskusjon. Oppmuntre elevene til å forklare strategiene sine.
- Utvikle telling med sprang for gangerekkene (f.eks. 4, 8, 12, 16, …).
- Se sammenhenger mellom gangerekkene.
- Utvid til større tall og divisjon for de elevene som trenger ekstra utfordringer.
- Elevene kan bruke en lommeregner til å få fram og kontrollere svarene sine. For eksempel kan de på en enkel måte lage multipla av 7 ved å trykke 0 + 7, og så trykke «= tasten» flere ganger. Slik kan de raskt kontrollere sin egen regning.
Ha som mål at elevene skal kunne multiplikasjonstabellen godt før de begynner med multiplikasjon av to- og tresifrede tall.
Viktige sammenhenger, som bør være kjent for alle elever:
- Multiplikasjon og addisjon: 3 ∙ 4 = 4 + 4 + 4.
- Den kommutative lov: 3 ∙ 4 = 4 ∙ 3. Best synliggjort ved å tegne et rektangel med sider 3 og 4, eller legge gjenstander i rektangelform med 3 ∙ 4 rader.
- Multipla av 2, 4 og 8: 4-gangen framkommer ved dobling av 2-gangen, og 8- gangen ved dobling 4-gangen.
- Multipla av 2 og 6 og 3 og 6: 6-gangen får en ved å tredoble 2-gangen, eller ved å doble 3-gangen.
- Multipla av 3 og 9: Multipla av 9 får en ved å tredoble 3-gangen.
- Multipla av 5 og 10: 10-gangen får en ved å doble 5-gangen. 5-gangen får en ved å halvere 10-gangen.
I multiplikasjonstabellen kan vi finne mange mønster. Denne tabellen er satt opp motsatt vei av det som er vanlig i de fleste norske lærebøker.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
- Summer et hvilket som helst tall fra første rad med tallet rett nedenfor i andre rad. Da får du tallet nedenfor i tredje rad. Det er fordi du summerer 1 ganger tallet med 2 ganger tallet, og da får vi 3 ganger tallet.
- Summer et tall i andre rad med tallet rett nedenfor fra femte rad. Da får du tallet nedfor i sjuende rad. Hvorfor?
- Lag et vilkårlig stort rektangel ved å starte i øverste venstre hjørne. Ruta i nederste høyre hjørne angir antallet ruter i rektangelet, mens kolonnen til høyre og raden i bunnen teller med sprang opp til dette tallet. Lag for eksempel et rektangel som er 5 ruter langt og 4 ruter høyt. Tallet i nederste høyre rute er 20, og det er antall ruter i rektangelet. Høyre kolonne teller 5, 10, 15, 20, mens raden i bunnen er 4-gangen: 4, 8, 12, 16, 20.
- Kvadrattallene ligger langs diagonalen fra øverste venstre hjørne til nederste høyre hjørne.
- Ta utgangspunkt i et hvilket som helst kvadrattall og gå ei rute til venstre og ei rute ned. Dette tallet er lik kvadrattallet minus 1.
- Ta hvilket som helst tall i et 2 ∙ 2 - kvadrat. Multipliser motstående diagonalhjørner, og produktene blir like. Et eksempel fra nest øverste venstre hjørne: 3 ∙ 8 = 6 ∙ 4.
Her er et eksempel på en aktivitet som gir øvelse i 6-gangen. Litt algebra gjør det mulig å lage liknende kretser for andre gangerekker:
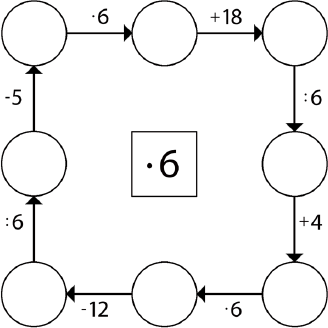
Elevene plasserer det tallet de vil i sirkelen øverst til venstre, og fyller ut de andre sirklene (med klokka) rundt hele kvadratet. Hvis de regner riktig, skal de ende opp med det tallet de begynte med. Hvis de begynner med 5 i sirkelen øverst til venstre, vil de måtte skrive 5, 30, 48, 8, 12, 72, 60, 10, 5. Noen elever kan synes det er spennende å lage sin egen «løype». Hvis de bruker prøving og feiling, er det ikke så enkelt som det kan se ut til.