Kobling mellom håndboka og kartleggingstestene

6.1 Forstå prosent (7, 8, 9, 10)

Introduksjon

Når vi skal innføre prosentbegrepet, er det tre sentrale aspekter vi må belyse:prosenttallet, det hele (representert som 100 %) og andelen av det hele somprosenttallet representerer. Mye av utfordringen i prosentregning er å få oversikt overhva det egentlig spørres etter i en oppgave. Eleven må kunne systematisereopplysningene.

Et viktig skritt på vei mot økt tallforståelse er det å raskt kunne se at 54 % er litt merenn halvparten, og at 97 % er nesten det hele. Denne forkunnskapen er en viktigforutsetning for å gjenkjenne prosent i ulike situasjoner.

Eksempler på misforståelser og misoppfatninger

• Noen tror at 20 % økning av et tall, etterfulgt av en reduksjon på 20 %, vil føretilbake til det opprinnelige tallet: Sykkelen kostet 2000 kr. Prisen økte med 20 %,for så å bli redusert med 20 %. Da vil prisen fortsatt være 2000 kr.
• En annen sentral misoppfatning er at å addere 10 % av en del med 10 % av enannen del, vil utgjøre 20 % av de kombinerte delene: På vår skole bruker 10 % avguttene og 10 % av jentene briller. Det betyr at 20 % av elevene våre brukerbriller.
• Mange elever blander sammen det å legge til x antall enheter, med det å legge tilx %: En økning på 15 % av 150 er 15 mer, og det blir til sammen 165.
• I mange sammenhenger blander elevene sammen addisjons- ogmultiplikasjonsaspektet: Prisen på huset er doblet. Det er 200 % prisøkning.

Anbefalinger og gode spørsmål

Rutenett

Begynn med å bygge opp en begrepsmessig forståelse av prosent som deler av 100 ved for eksempel å bruke et 10 ⋅ 10 rutenett (figur 6.1.). 20 % kan visualiseres slik:

Skraver områdene som representerer forskjellige prosentandeler. Bruk dette til å bygge opp erfaringsreferanser rundt sentrale prosentandeler, som 50 %, 25 %, 10 %, 20 % og 1 %. Fokuser også på «det som er igjen»:

• Du har skravert 10 %. Hvor stor del har du ikke skravert?
• Du drikker 25 % av juicen. Hvor mange prosent er igjen?

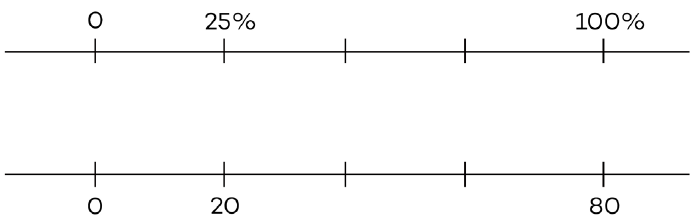
Tallinje

Doble tallinjer er nyttige hjelpemidler for å skape mentale bilder for å sammenligne prosenter og tall.

Eksempel: «Her er to tallinjer. Jeg har markert 25 %. Hvor mye er 25 % av 80?»

Tellebrikker og kuber

Tellebrikker og kuber er nyttige for å konkretisere økning og reduksjon i prosent. Dethele tallet bør velges med omhu, slik at tallene går opp.

Eksempler på misforståelser og misoppfatninger

Ta utgangspunkt i 8 tellebrikker. Å øke med 25 % betyr å legge til 2 tellebrikker. Dahar vi totalt 10 tellebrikker, som nå er 100 %. For å komme tilbake til 8 må vi fjerne 2av de 10. Det er en reduksjon på 20 %. I dette eksempelet ser vi at en økning på 25% gjør at en må redusere det «nye» tallet med 20 %, for å komme tilbake tilutgangspunktet.

Bygg strategier for å beregne prosenten ved å bruke erfaringsreferanser, foreksempel:

22 % av 80 er 10 % + 10 % + 2 % av 80. Løsningen blir: 8 + 8 + 1,6 = 17,6.Løsningen kan langt på vei kontrolleres ved å bruke overslag eller hoderegning. 22% er mindre enn 25 %, altså mindre enn en firedel av 80, som er 20, så løsningen ersannsynlig.

Vis med tellebrikker:

• en økning på 25 % av 12
• en reduksjon på 20 % av 15
• 120 % av 5
• 300 % økning av 4

• Hvor mye er en økning på 50 % av 30 kr?
• Hva er 150 % av 8 kr?
• Hva er en reduksjon på 10 % av 50 kr?
• Kan du ha mer enn 100 %?